Machine Learning Inference on Inequality of Opportunity

Is inequality unfair?

Based on research by Juan Carlos Escanciano and Joël Terschuur

Are there fair and unfair economic inequalities? If so, can we define, measure, and make inferences on “unfair inequality”? On the one hand, unequal returns might foster effort and innovation. On the other hand, an uneven distribution of life outcomes such as income, wealth, education, or health can lead to unrest and political polarization. A concept that has gained broad consensus is Inequality of Opportunity (IOp). Inequalities that are explained by circumstances outside the control of the individual are generally deemed unfair and constitute IOp. It is precisely the unchosen nature of circumstances that fuels a debate on gender gaps, racial discrimination, or the importance of parental resources for many vital outcomes. Furthermore, inequalities based on circumstances instead of effort might entail an important waste of talents and capabilities. It becomes clear that a rigorous quantification of IOp is crucial for an informed debate.

Following a well-grounded theoretical and normative framework developed in the seminal contributions to political philosophy and economics by Fleurbaey (1995) and Roemer (1998), among others, economists have tried to provide quantitative measures of IOp. The main idea is that if one can predict an individual outcome using circumstances, then there is IOp. By predicting outcomes with circumstances and then measuring the inequality in the distribution of predictions, we can quantify IOp. For example, suppose that the income of any individual was the same as the income of his/her parents. Then, we would perfectly predict income given parental income, and the inequality in the predictions would be the same as income inequality, i.e., all income inequality would be explained by circumstances.

An ongoing problem of the IOp literature is how to fully exploit the information of all observed circumstances. There has always been a trade-off between the number of circumstances to include in the analysis and the sample size of existing datasets. Traditional estimation methods have made it either prohibitively costly to include all observable circumstances (e.g., non-parametric methods) or imposed far too much structure on the relationship between the outcome and the circumstances (e.g., linear regression). Only recently, machine learning (ML) techniques, which can handle high dimensional problems, have been employed to overcome this long-lasting problem. The impressive performance of machine learners, such as random forests, boosting, lasso, or neural networks, among many others, serves to obtain high-quality predictions of the outcome given a data-driven selection of circumstances in a first step. In the second step, the inequality of the predictions is measured, with the Gini of the predictions being one of the preferred measures of IOp.
This is the starting point of our research. The use of ML for IOp measurement is still in its cradle. We stress that ML opens many possibilities but must be used with care. ML boils down to trading off bias and variance of predictions. In Figure 1, we see that we can get very good in-sample predictions by overfitting (connecting the dots), but this will have a very high variance and perform badly in new samples. We can also underfit and have no variance but a lot of bias.

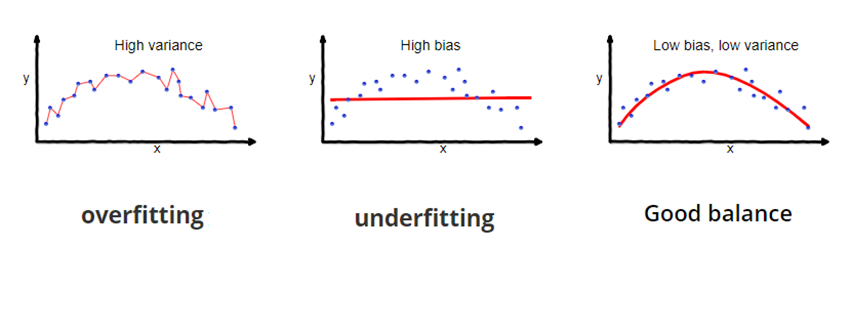
^{Figure 1 Bias and Variance trade-off}

^{Source: towardsdatascience.com}

While this trade-off is essential for good prediction, it becomes problematic for estimating IOp. This is because allowing for bias in the first step prediction will generally lead to bias in the second step estimation of IOp. To see that this can matter, we simulate many artificial samples, and in each sample, we estimate IOp with an estimator that does not take into account ML bias, the plug-in estimator, and our proposed debiased estimator. Since the samples are simulated, we know the true level of IOp, and we can subtract this from our estimates so that we would expect the distribution of these estimates to be centered around zero. Figure 2 shows the results of this exercise. In an ideal setting, one would want centered estimates distributed as the red line. We see that the debiased estimates approximate this line while the plug-in estimates are completely off.

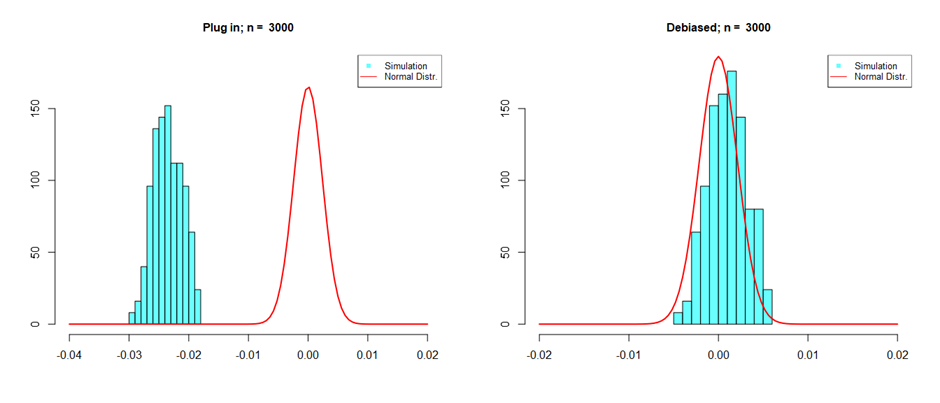
^{Figure 2 ML bias in IOp measurement}

In our paper, we develop a general methodology to construct estimators that are robust to such biases and provide their inferential properties. Inference on IOp, i.e., quantifying uncertainty of estimates through standard errors or confidence intervals, has been an elusive objective in the IOp literature, and usually, no such quantifications are reported. The use of ML only makes this harder. Applying our general methodology, we propose a simple debiased IOp estimator for which applied researchers can easily compute confidence intervals and perform statistical tests even when ML is used. We motivate the general methodology through its application to IOp since this was what first motivated the paper. However, our methods apply to many other interesting economic examples, such as semiparametric gravity models in international trade or algorithmic fairness.

We take our methods to the data to measure IOp in different European countries. We use the 2019 cross-sectional European Union Statistics on Income and Living Conditions (EU-SILC) survey. This survey is one of the main references for the analysis of income distribution and poverty in Europe. It includes a module on intergenerational transmission of disadvantages with rich information on circumstances relating to the individual’s life/household when he/she was around 14 years old. Among others, we use circumstances such as sex, country of birth, whether he/she was living with the mother/father, the number of adults/working adults/kids in the household, the population of the municipality, tenancy of the house, country of birth of the parents, nationality of the parents and education of the parents.

In Figure 3, we see the estimates of the share of total inequality explained by circumstances in different European countries. Black solid dots are debiased estimates using our methodology with their corresponding 95% confidence interval. Hollow red symbols are the estimates that blindly use ML, the plug-in estimates, without taking care of the ML-induced bias.

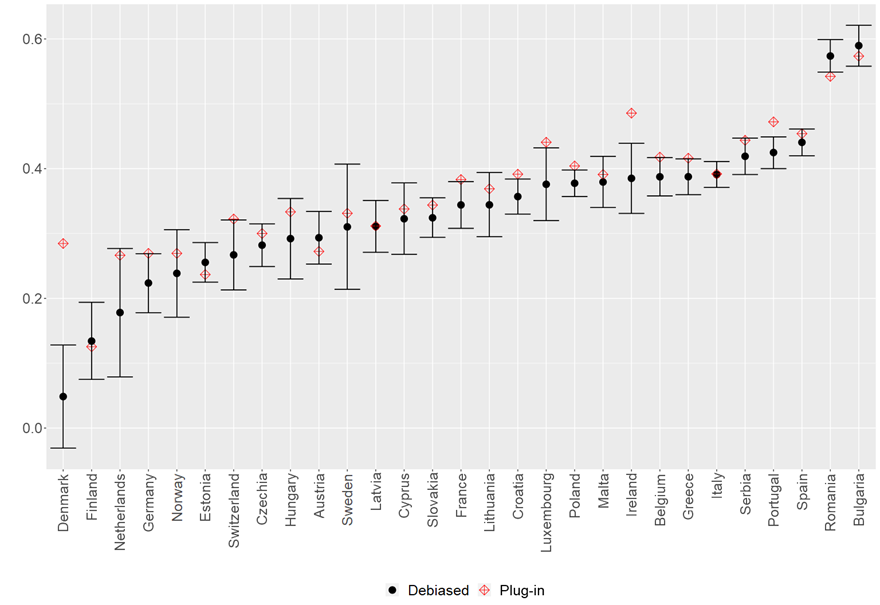
^{Figure 3 IOp in Europe}

The countries with the highest IOp are Romania and Bulgaria, where around 60% of income inequality can be explained by circumstances, while Denmark is the country with the lowest IOp. Nordic countries, Germany, the Netherlands, and some Eastern countries have low IOp. Southern countries have high IOp, with Greece and Italy having 39% and Spain having 43% of total inequality explained by circumstances. We find that the plug-in estimator tends to overestimate IOp in general, and particularly so for Denmark. The difference between our debiased estimates and the biased plug-in estimates of IOp can be as large as 25 percentage points in the case of Denmark. In the rest of the countries, the difference is smaller, but we still observe differences of 5-10 percentage points. Hence, plug-in estimators give a biased view of IOp in Europe.

One important advantage of using our proposed debiased estimator is that the final estimate becomes less dependent on which ML algorithm one uses. A priori, it is hard to tell whether one should use Random Forests to predict a Boosting algorithm or some Neural Network. Hence, one would not want the result to change too much by changing the ML algorithm used for predictions. In Figure 4, we see the IOp debiased and plug-in estimates for the different countries using different machine learners. Again, the solid-colored dots represent our debiased estimator, and the hollow symbols are the plug-in estimator that does not consider ML-induced bias. We can see how the debiased estimates are much closer to each other and, hence, less dependent on the ML algorithm used. Conversely, using different ML algorithms with the plug-in estimator can lead to wildly different IOp estimates.

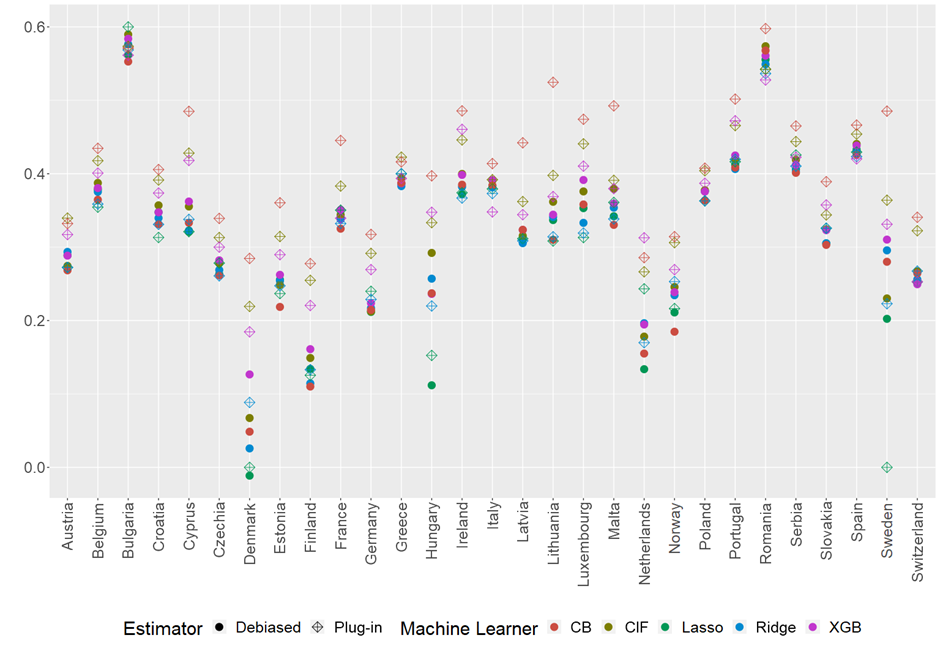
^{Figure 4 Sensibility to the choice of ML algorithm}

In conclusion, ML opens an array of possibilities but must be used with care. We must not forget the importance of inference, and we should use estimators that are robust to the choice among the myriad of ML algorithms out there.

Machine Learning Inference on Inequality of Opportunity

Further Reading:

Related Posts

Quantitative Analysis of Climate Heterogeneity

Are we entering a new glaciation period? Forecasting long-run climate change with paleoclimate data