Econometric techniques as alternative to complex Global Circulation Models
Based on research by Andrey Ramos
Climate change heterogeneity
Climate change dynamics are non-uniform across space and time. For example, not all regions of the globe are warming at the same rate. Surface air temperature over the Arctic is increasing twice as fast as the global average, a phenomenon known as Arctic Amplification (AA) (You et al., 2021). More broadly, equatorial regions have, on average, experienced slower warming compared to northern latitudes. As shown in Figure 1, some areas, such as Alaska, north of Europe, and Siberia, have seen temperature increases exceeding 3C over the past 50 years, while regions closer to the equator have experienced almost negligible changes. Even within a constant spatial dimension, empirical evidence shows significant seasonal heterogeneity with winter temperatures rising faster than summer temperatures (Hillebrand and Proietti, 2017).
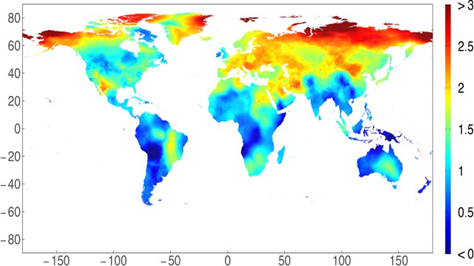
Figure 1: Fitted linear trend change in local temperatures between 1970 and 2019, Desmet and Rossi-Hansberg (2024)
Climate heterogeneity has important implications for the climate system and the economics of climate change. From a climate system perspective, AA accelerates sea ice cover reduction over the Arctic Pole (Kwok, 2018) and permafrost1 degradation. Additionally, a growing body of research suggests that AA has contributed to the increased frequency of extreme weather events, including severe cold winters, heatwaves, and intense precipitation or snowfall in other latitudes (Zhang et al., 2020). From an economic standpoint, Brock and Xepapadeas (2017) demonstrates that overlooking AA in economic models could lead policymakers to under- estimate the optimal tax on greenhouse gas emissions. Accurately accounting for climate heterogeneity is also essential for better anticipating the localized impacts of climate change.
An econometric model to quantify climate heterogeneity
Econometric modeling of climate systems can contribute to a deeper understanding of climate heterogeneity and its implications through the development of quantitative methodologies moving beyond considering the annual average temperature as a sufficient statistic for global climate change. My research, aligned with the recent contribution of Gadea and Gonzalo (2020), focuses on the modeling and forecasting of the dynamics of the entire temperature distribution. Concretely, I propose a statistical multivariate Vector Error Correction Model (VECM) for a range of unconditional distributional characteristics of temperature (mean and quantiles) and the total radiative forcing2, including the radiative forcing of anthropogenic greenhouse gases like the carbon dioxide (CO2). Noticing that the unconditional quantiles of temperature correspond to temperatures at different latitudes (or seasons), this simple and flexible approach allows for the quantification of various forms of climate heterogeneity.
The proposed methodology has several key features. First, the vector error correction model is derived from a statistical discrete-time approximation of a One-Dimensional Energy Balance Model3 (EBM) (Held and Suarez, 1974). Second, the estimation and testing procedures are robust to different types of trends (whether stochastic or deterministic) present in the data. Third, the methodology is flexible enough to be applied at various scales (global, hemispheric, continental, national, or even at the city level) provided there is sufficient cross- sectional variation or high-frequency observations to estimate temperature quantiles over time. Fourth, once the model is estimated, it is possible to generate outcomes of practical interest, including
i) estimation of physical parameters, such as quantile-dependent climate sensitivities;
ii) long-term density forecasts of temperature;
iii) identification of distributional shocks and impulse-response analysis; and iv) projections of temperature distribution under hypothetical emissions or concentration scenarios.
An alternative to Global Circulation Models
To demonstrate the applicability of the methodology, I conduct an empirical analysis utilizing station-level temperature data from the latest version of the HadCRUT5 dataset4 (Morice et al., 2021), along with radiative forcing data from Hansen et al. (2011). Focusing on a set of stable stations in the Northern Hemisphere that have been continuously observed from 1880 to 2022, I calculate both the average and the quantiles of the temperature distribution each year and estimate the unconditional quantile VECM. Empirical findings document strong heterogeneity in the dynamics of the hemispheric temperature distribution. Estimated climate sensitivities5, depicted in Figure 2, are heterogeneous across the temperature distribution. For quantile 5% (representing the coldest temperatures), the confidence interval for the climate sensitivity ranges from 2.82 C to 4.51 C, while for quantile 95% (representing the warmest temperatures) the range of variation is from 1.31 C to 1.79 C. The distinct, non-overlapping confidence intervals across quantile levels suggest significant differences. Focusing on Figure 3, projections of the temperature distribution conditional on a range of hypothetical Shared Socioeconomic Pathways (SSP)-based concentrations scenarios6 suggest non-uniform expected increases in temperature across the distribution.
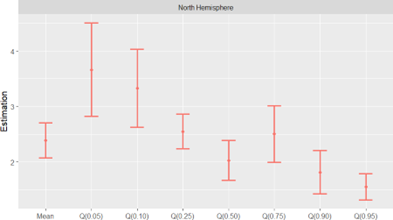
Figure 2: Distributional Climate Sensitivities
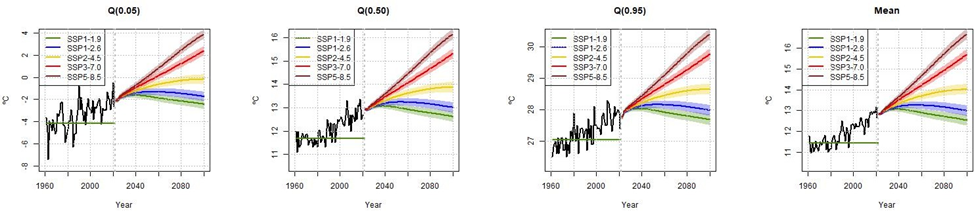
Figure 3: Long-term projections of temperature conditional on selected SSP scenarios
An alternative to producing this type of estimation and projection outcomes is to use simulations from complex large-scale General Circulation Models (GCMs).7 In the GCMs approach, the climate sensitivity is often determined by simulating a known radiative forcing change (e.g., doubling CO2) and computing the resultant temperature change with respect to an initial equilibrium (Knutti et al., 2017). Recent estimates place climate sensitivity likely between 2 C and 5 C, with the uncertainty reflecting a range of possible outcomes depending on feedback strengths and interactions within the climate system. For forecasts or scenario projections, climate scientists simulate GCMs assuming future paths of emissions or concentration scenarios and provide uncertainty measures by running the model multiple times from slightly different initial conditions (Lupo et al., 2013; AR6- IPCC, 2021). Due to their complexity, GCMs are computationally expensive to solve and heavily dependent on the initial conditions of the system. Moreover, simulating these models requires a large amount of input data and a coupling of various sub-models.
Observational time-series methodologies and GCMs are complementary in a similar way to the complementarity in economics between Structural VAR (SVAR) methods and Dynamic Stochastic General Equilibrium (DSGE) models. While DSGE models aim to provide a detailed description of all interactions in the economy, SVAR models start with a plausible time-series representation of the data and impose minimal restrictions to make meaningful inferences. In the context of the current research, the unconditional-quantile VECM achieves a desirable balance between a purely statistical multivariate approach and the theoretical/structural modeling of the climate system, allowing the production of estimation and projection results and for the assessment of estimation uncertainty in a simpler statistical reduced-form procedure.
Main message
Climate change heterogeneity is relevant and must be incorporated into economic studies. The methodological contribution of this paper provides researchers with a simple reduced-form statistical tool to empirically quantify the degree of heterogeneity in the temperature distribution, offering estimates and projection outcomes that can expand the scope of climate economics research. For instance, the estimated climate sensitivities and their associated confidence intervals are useful for calibration and uncertainty analysis in integrated assessment models with geographical heterogeneity (such as Krusell and Smith (2022) or Cruz and Rossi-Hansberg (2024)). Long-term density projections under different scenarios, on the other hand, are important inputs for estimating global and local damages from climate change while accounting for heterogeneity. The potential application of this methodology across various geographical scales opens the door to a new type of research focusing on the evolution of the entire temperature distribution and its economic consequences. This approach enables the production of research findings to better inform adaptation and mitigation policies.
About the author: Andrey Ramos is a final-year PhD Student in Economics at UC3M interested in time series econometrics, quantitative climate economics, and applied econometrics.
Further reading:
Ramos, A. (2024) Quantitative Analysis of Climate Heterogeneity via anUnconditional Quantile Vector Error Correction Model, Job Market paper.
References:
- AR6-IPCC (2021). Climate Change 2021: The Physical Science Basis. [Masson-Delmotte V, Zhai P, Pirani A et al. (eds)]. Cambridge and New York: Cambridge University Press.
- Brock, W. and A. Xepapadeas (2017). Climate Change Policy Under Polar Amplification. European Economic Review 94, 263–282.
- Cruz, J.-L. and E. Rossi-Hansberg (2024). The Economic Geography of Global Warming. Review of Economic Studies, forthcoming .
- Desmet, K. and E. Rossi-Hansberg (2024, March). Climate Change Economics over Time and Space. Working Paper 32197, National Bureau of Economic Research.
- Gadea, M. and J. Gonzalo (2020). Trends in Distributional Characteristics: Existence of Global Warming.
- Journal of Econometrics 214, 153–174.
- Hansen, J., M. Sato, P. Kharecha, and K. von Schuckmann (2011). Earthˆas Energy Imbalance and Implications.
- Atmospheric Chemistry and Physics 11, 13421ˆa13449.
- Held, I. M. and M. J. Suarez (1974). Simple Albedo Feedback Models of the Icecaps. Tellus 26 (6), 613–629.
- Hillebrand, E. and T. Proietti (2017). Phase Changes and Seasonal Warming in Early Instrumental Temperature Records. Journal of Climate 30 (17), 6795 – 6821.
- Knutti, R., M. A. Rugenstein, and G. C. Hegerl (2017). Beyond Equilibrium Climate Sensitivity. Nature Geoscience 10 (10), 727–736.
- Krusell, P. and A. Smith (2022). Climate Change Around the World. Working Paper 30338, National Bureau of Economic Research.
- Kwok, R. (2018, oct). Arctic Sea Ice Thickness, Volume, and Multiyear Ice Coverage: Losses and Coupled Variability (1958ˆa2018). Environmental Research Letters 13 (10), 105005.
- Lupo, A., W. Kininmonth, J. Armstrong, and K. Green (2013). Global Climate Models and Their Limitations.
- Climate change reconsidered II: Physical science 9, 148.
- Morice, C. P., J. J. Kennedy, N. A. Rayner, J. P. Winn, E. Hogan, R. E. Killick, R. J. H. Dunn, T. J. Osborn,
- P. D. Jones, and I. R. Simpson (2021). An Updated Assessment of Near-Surface Temperature Change From 1850: The HadCRUT5 Data Set. Journal of Geophysical Research: Atmospheres 126 (3), e2019JD032361.
- You, Q., Z. Cai, N. Pepin, D. Chen, B. Ahrens, Z. Jiang, F. Wu, S. Kang, R. Zhang, T. Wu, P. Wang, M. Li,
- Z. Zuo, Y. Gao, P. Zhai, and Y. Zhang (2021). Warming Amplification over the Arctic Pole and Third Pole: Trends, Mechanisms and Consequences. Earth-Science Reviews 217, 103625.
- Zhang, R., C. Sun, J. Zhu, R. Zhang, and W. Li (2020). Increased European Heat Waves in Recent Decades in Response to Shrinking Arctic Sea Ice and Eurasian Snow Cover. Climate and Atmospheric Science 3 (1), 620–621.
———————————————————————————-
- Permafrost refers to soil that remains at or below the freezing point of water for two or more years. Permafrost regions cover about 24% of the exposed land surface in the Northern Hemisphere. ↩︎
- Radiative forcing is a concept used in climate science to quantify the energy imbalance in Earth’s atmosphere caused by anthropogenic activities or natural events. Since the start of the industrial era until the present day, anthropogenic forcing has typically been increasing and has been the dominant component of the total forcing on the Earth system except for brief periods following large volcanic eruptions. ↩︎
- Energy Balance Models are theoretical climate models that describe changes in temperature as a function of the imbalance between incoming solar radiation and outgoing radiation emitted by the planet. ↩︎
- The dataset is developed by the Climatic Research Unit (CRU) at the University of East Anglia and the Hadley Centre at the UK Met Office, accessible at the following URL:https://crudata.uea.ac.uk/cru/data/temperature/ ↩︎
- The climate sensitivity refers to the long-term change in temperature in response to a doubling in the CO2 concentrations. ↩︎
- A SSP scenario describes a potential future development path, grounded on a coherent and internally consistent set of assumptions regarding driving forces like demography, economic processes, technological innovation, and their wide-ranging implications for energy use, land utilization, and emissions (AR6-IPCC, 2021) ↩︎
- GCMs are complex computer simulation models based on mathematical equations representing various features of the Earth’s climate system, including interactions between the atmosphere, oceans, land surface, and ice. These models are essential tools for studying the climate system and predicting future changes (Lupo et al., 2013). ↩︎



