Firms not only produce and collude…. They kill each other…
By Carmen Beviá, Luis C. Corchón and Yosuke Yasuda
“People of the same trade seldom meet together, even for merriment and diversion, but the conversation ends in a conspiracy against the public, or in some contrivance to raise prices”.
Adam Smith, An Inquiry into the Nature and Causes of the Wealth of Nations.
A constant concern among the general public and policymakers is the possibility that firms synchronize their plans and achieve larger profits than those warranted by competition, i.e., they collude (see an example here). Given that firms cannot write legally binding contracts, the question is to explain under which mechanism firms can achieve collusion. This is one of the goals of the so-called folk theorem. This theorem has many versions (see one here). Here, we will be content to provide a short non-technical definition.
Suppose a given number of firms (or, in general, agents) that repeatedly play a certain game. There is no date at which this situation will end. The firm’s objectives are summarized by the sum of discounted payoffs. Strategies are mappings from the set of histories into one-period actions. The usual notion of a Nash equilibrium applies to these strategies. Sometimes, a stronger notion of equilibrium is used, namely, the Subgame Perfect Nash Equilibrium, in which the strategies must be a Nash Equilibrium for any history. This refinement rules out threats that firms have no incentive to carry out when the time comes. The folk theorem says that:
When firms discount very little future payoffs (i.e., when firms are patient), any payoff above the mini-max payoff can result as a Nash or a Subgame Perfect Nash Equilibrium.
In particular, if we assume that firms can communicate before the game starts, it seems natural to assume that they will choose strategies that sustain equilibrium payoffs on the Pareto frontier. This is how rational agents, who cannot draft binding contracts, can achieve collusion.
The previous result assumes that firms will remain in the game indefinitely. However, we observe that firms can go bankrupt and often do. A new twist on bankruptcy emerges: the possibility that one firm takes actions specifically to promote the bankruptcy of others. We term this situation “Strategic Bankruptcy”.
Our previous paper on this matter (Beviá et al., 2020) found that with two firms with different constant average cost functions, the static Cournot equilibrium outcome could not be sustained as an Equilibrium because firms have incentives to predate. In those cases, there is a Markov perfect equilibrium in mixed strategies in which one firm will eventually be bankrupt and driven out of the market with probability one. The presence of potential bankruptcy makes the set of outcomes supportable via tacit collusion different than in the absence of bankruptcy.
In this paper, Beviá et al. (2023), we examine the relationship between Nash and Subgame Perfect Nash Equilibria in games with an infinity horizon and the concept of Bankruptcy-Free (BF) allocations defined as the set of outputs in which no firm can ruin another firm without ruining itself. In Figure 1, outputs are denoted by x1 and x2. The solid (resp. dotted) thick straight line denotes the pairs of zero profit for firm 1 (resp. 2), and the area below these lines corresponds to the pairs of outputs that allow positive profits. The dashed lines represent best replies. The set BF is the square [0, 10/7] X [0, 50/7], where the point (10/7, 50/7) is the intersection of the two zero profit lines. The reader can check that if both firms choose outputs in this square, any unilateral deviation of a firm that drives the rival to bankruptcy also drives the deviating firm to bankruptcy.
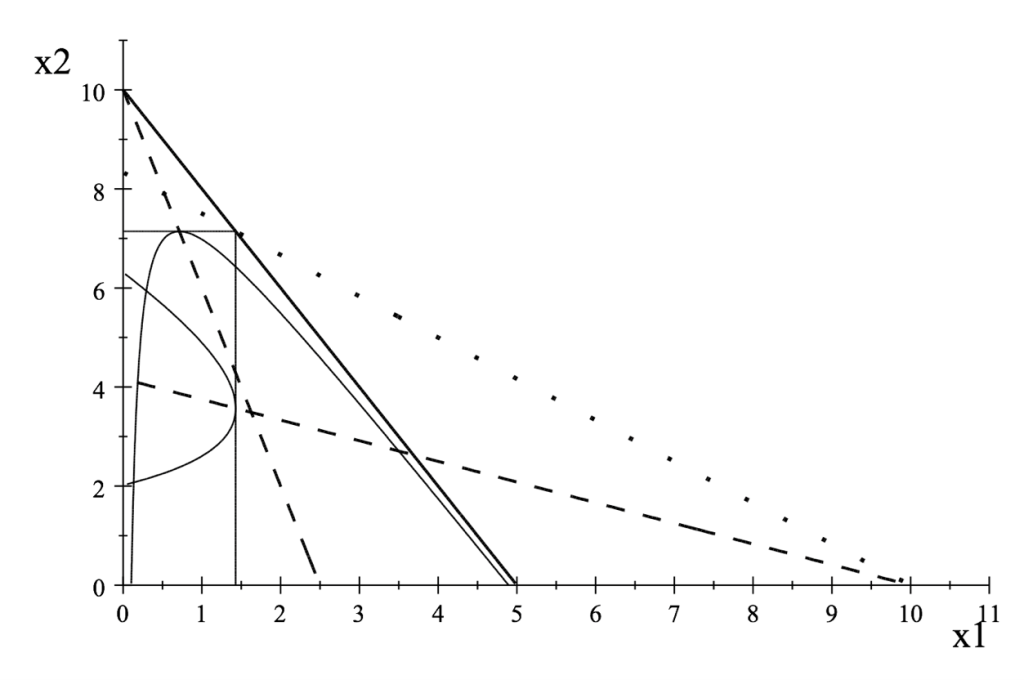
Figure 1
Our first result is that when two firms are very patient, under a boundary condition (that implies that the outputs of firms cannot converge to zero very quickly), any Nash equilibrium of the game with an infinity horizon must yield in each period outputs that are Bankruptcy-Free (BF). The reason is that if a firm chooses an output outside the BF set, it can be driven to bankruptcy. The surviving firm obtains monopoly profits forever. If the firm is very patient, this allows the firm to overcome any possible profit loss of the move that precipitated the bankruptcy of the rival. In Figure 1, the Cournot equilibrium (at the intersection of the dotted lines representing best replies) is not BF. This implies that, if firms are very patient, the Cournot equilibrium cannot be supported as a Nash Equilibrium.
We also provide examples showing that the assumptions made in this result are tight. Specifically, the result does not hold true for three firms. If these firms collude, but equilibrium strategies for all firms dictate cut-throat competition when there are only two firms, there are no incentives to eliminate a competitor due to the repercussions in a duopolistic market. Furthermore, if the boundary condition is not met, it might not be advantageous to bankrupt a firm that will become irrelevant in the long run.
Having cleared the relationship between incentives (equilibrium) and bankruptcy (BF), we proceed to prove the Folk Theorem within our framework, assuming increasing average costs. Our prior findings indicate that we need to replace the condition on minimax payoffs with minimax BF payoffs (minimax payoffs obtained in the set of BF allocations). They differ from the standard minimax concept because firms cannot harm other firms with outputs that lead to their own bankruptcy. In Figure 1, we see that the set of mini-max BF payoffs results from outputs inside the two thin curves. When firms are very patient, any list of payoffs below mini-max BF payoffs cannot be supported as a Subgame Perfect Nash equilibrium.
Define a feasible payoff as one such that there is a BF output profile that yields this payoff. Recall that this is different from the definition of the original Folk Theorem, where a feasible payoff is just a payoff that is yielded by some outputs. Then, we prove a Folk Theorem restricted to feasible payoffs that reads as follows:
Any list of feasible payoffs above the mini-max BF can be sustained as a Subgame Perfect Nash equilibrium when firms are sufficiently patient.
What happens when payoffs are not feasible (i.e., no BF output yields these payoffs)? As we saw in the example above with three colluding firms, it is possible to sustain payoffs that are not feasible by making competition sufficiently harsh when a firm is driven out of the market. So, we have our second folk theorem that is not restricted to feasible payoffs but needs a stronger condition on mini-max BF, namely that payoffs are larger than any mini-max BF calculated not only in the set of original firms but in every subset of it.
With more than two firms, payoffs above the mini-max BF payoffs for the set of firms and any possible subset of firms, can be sustained as a Subgame Perfect Nash equilibrium if firms are sufficiently patient.
Summing up, the possibility of Strategic Bankruptcy introduces new twists in the venerable folk theorem. Under duopoly, the possibility that firms engage in predatory activities must be accounted for. The worst possible outcome must take into consideration that firms will never punish other firms beyond the limits of BF allocations. In short, under possible predatory activities, collusion is not as easy to sustain as we previously thought! Our analysis also points out that mergers from three to two firms may cause a change in the structure of the industry.
Our analysis has abstracted from several important features such as accumulation, coalitions, credit, entry, and buying competitors (see more on this in our remarks at the conclusion of our 2020 paper). But the purpose of our present paper is to show that the introduction of predation is tractable and offers new insights into the theory of competition.
Further Reading:
Beviá, C., and L. Corchón. “Dynamic Contests With Bankruptcy: The Despair Effect.” B.E. Journal of Theoretical Economics, 16, 1, 217-241, 2016.
Beviá, B., L. Corchón and Y. Yasuda. “Oligopolistic Equilibrium and Financial Constraints”. Rand J. Economics 51, 1, 279-300, 2020.
Beviá, B., L. Corchón and Y. Yasuda. “Folk Theorem under Bankruptcy”. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4592166
Dargaud, E., M. Menuet, M., and P. G. Sekeris (2023). “Collusion and Predation under Cournot Competition”. Managerial and Decision Economics, forthcoming.
Fudenberg, D. and E. Maskin. “The Folk Theorem in Repeated Games with Discounting or with Incomplete Information”. Econometrica , 54, 3, 533-554, 1986.
About the authors:
Carmen Beviá works in game theory applied to Contests and Social Choice. https://cvnet.cpd.ua.es/curriculum-breve/es/bevia-baeza-carmen/55994
Luis Corchón works in game theory applied to Contests and Industrial Organization. https://www.eco.uc3m.es/english/staff/cv/lcorchon.html
Yosuke Yasuda works in game theory applied to Industrial Organization and Matching. https://yagena.github.io/



